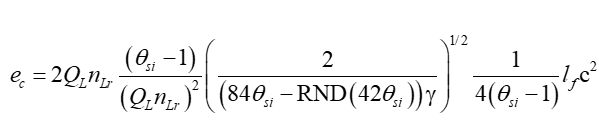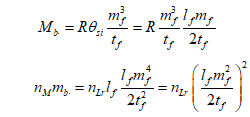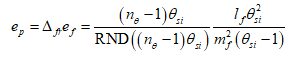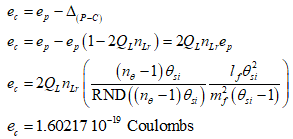describing Elementary Charge
using only the FUNDAMENTAL MEASURES
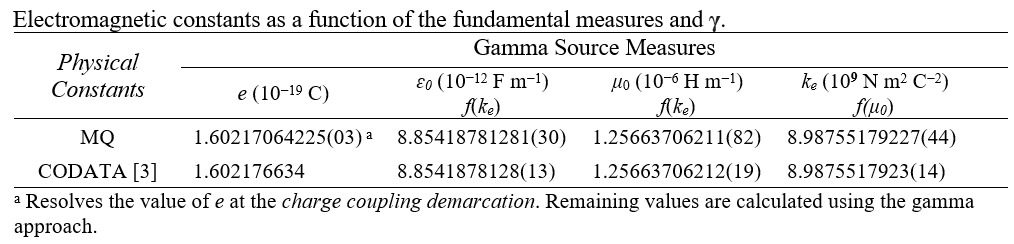
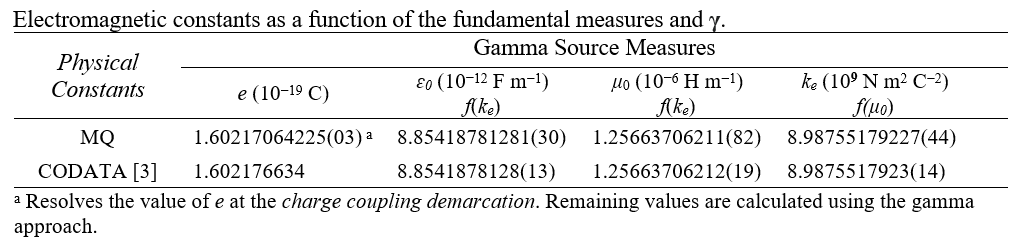
CODATA
MQ
1.602176634 10-19 C
1.60217064225(03) 10-19 C
Inputs
- θsi can be measured as the polarization angle of quantum entangled X-rays at the degenerate frequency of a maximal Bell state. As an angle θsi=3.26239 rad ± 2 μrad; as a momentum θsi=3.26239030392(48) kg m s-1 and with respect to the Target Frame, θsi has no units. The relation of angle and mass is mathematically demonstrated, as well, by No-Ping Chen, et. al.
- lf, mf and tf are the fundamental measures, more precise expressions for Planck’s units – length, mass, and time – that consider the effects of length contraction associated with discrete measure.
Terms
- c is the speed of light which may also be written as c=nLlf/nTtf=299,792,458 m/s such that nL=nT=1 is physically significant.
- QL is the fractional portion of a count of lf when engaging in a more precise calculation.
- nLr describes the count of lf representative of a change in position of an observable measured with respect to the observer’s frame of reference.
- Δf is the metric differential between frames.
- QLnLr, also known as the Informativity differential describes the length contraction associated with discrete measure.
- ɛ0 is the electric constant
- μ0 is the magnetic constant
- ef is the fundamental form of elementary charge, defined with respect to the Target Frame before adjusting for the metric and Informativity differentials.
- ep is the Planck form of elementary charge, defined with respect to the Measurement Frame, accounts for the metric differential between frames.
- ec is the classical form of elementary charge, accounts for the metric and Informativity differential.
- ħ is the reduced Planck constant, 1.054571817 10-34 m2 kg s-1. When accounting for the Informativity differential at the upper count bound, this term is not italicized (i.e., ħ=1.0545349844(45) -34 m2 kg s-1).
- αf-1 is the fundamental form of the inverse fine structure constant defined with respect to the Target Frame.
- αp-1 is the Planck-like form of the inverse fine structure constant defined with respect to the Measurement Frame.
- αc-1 is the classical form of the inverse fine structure constant as adopted by the CODATA collaboration. This term accounts for length contraction associated with discrete measure.
- Mb is the bound mass which represents the upper count bound of mf that can be measured per tf in a homogenous mass distribution.
- γ is a collection of terms that describe the geometry between the Target and Measurement Frames.
Calculations
Experimental Support
NIST: CODATA Recommended Values of the Fundamental Physical Constants: 2018, (May 2019), https://physics.nist.gov/cuu/pdf/wall_2018.pdf, doi:10.1103/RevModPhys.93.025010.
Discussion
It is difficult to resolve an expression for elementary charge for several reasons. Notably, with respect to the System Frame there is no known expression for charge consisting of only the fundamental measures. With respect to the Reference and Internal frames, there is also no known correlation of elementary charge to the fundamental measures: length, mass and time. For these reasons, developing a physically significant description of elementary charge in a Measurement Quantization (MQ) nomenclature requires an approximation, while at the same time retaining a physically significant instantiation.
We approach the problem with the equality of two expressions – one defined with respect to the non-discrete System Frame of the universe and the other defined with respect to the discrete Internal Frame – to resolve an expression that allows us to correlate the two frames(6,Sec. II.D). Specifically,
With this we then integrate elementary charge as a function of the fundamental measures, such that we resolve the fundamental expression for ef with respect to the non-discrete System Frame as a function of b.
We avoid issues with physical insignificance for two reasons. One, we know the difference value (i.e. 1) associated with the discrete System Frame and we know its corresponding non-discrete value associated with the Internal Frame. We also know the expression for momentum θsi=(1/2)lfmf/tf, indicating that we should divide by two, hence ħ/2. And, where we have previously resolved the mass frequency bound(3,Eqs. 81-83) as would describe a galaxy, we resolve the upper count bound(1,Eqs. 27-29) of mf with respect to the count of tf. This is further described in the third paper (3,Appx. 5.3).
Thus, we find that f(mf)=mf2 with respect to θsi=lfmf/2tf (i.e., the remaining terms). Mapping both to θsi, then b=mf2/(ħ/2). Using ħ=2θsilf we reduce. The approach confirms the identification of θsi as the divisor/difference d. Thus, we remove θsi from the base b and account for the squared relation of mf at the bound. And then we present a fundamental expression for elementary charge ef with respect to the non-discrete System Frame.
The process to present charge in terms of the local frame follows the same adjustments we implement in a derivation of the fine structure constant(6,Eq. 75) or any physically significant measure. First, we apply the metric differential. This is described as a product of the quantization ratio(6,Eq. 140) between the two frames. The frame difference is equal to one relative to the blackbody demarcation(6,Apx. C). We describe this as nθ-1 such that nθ=42.
The Planck equivalent of elementary charge is then.
Next, we account for the Informativity differential(6,Sec. II.G) relative to the blackbody demarcation(6,Apx. C) 84.6005496647(07)lf. This will allow us to resolve the difference between the Planck-like ep and classical forms of the elementary charge ec;
Subtracting the Informativity differential 2QLnLr of ep from ep (i.e., 1-2QLnLr), then
We compare the result with the 2018 CODATA value.
NIST: CODATA Recommended Values of the Fundamental Physical Constants: 2018, (May 2019), https://physics.nist.gov/cuu/pdf/wall_2018.pdf, doi:10.1103/RevModPhys.93.025010.
We have presented an expression describing elementary charge using only the fundamental measures(5,Sec. III.B). Notably, the result differs by one part in the sixth digit. There are two contributors to this variance. First, we have accounted for the Informativity differential(6,Sec. II.G) at the blackbody demarcation. This will effect precision in the eight digit. Second, we use the metric offset as a frame difference to then resolve the fundamental form of e. This would be correct if we had a Planck-like description of e in terms of the fundamental measures. We do not.
The approach taken does not arise from our classical understanding of charge, but instead resolves as a function of discrete offsets between subtractive and divisor relations at the lower count bound. The approach is physically significant, but not well understood. It is also incomplete.
That said, we find charge to be a function of m kg-2 accompanied by three geometries. The first is described by the Informativity differential 2QLnLr. The second is described by quantization ratios(6,Eq. 140) and allows translation of measures between the discrete and non-discrete frames. The third, describes the metric offset (i.e. 1) between frames. Collectively, the three geometries and the dimensional ratio m kg-2 describe the phenomenon we recognize as elementary charge.
Quantum Inflation, Transition to Expansion, CMB Power Spectrum