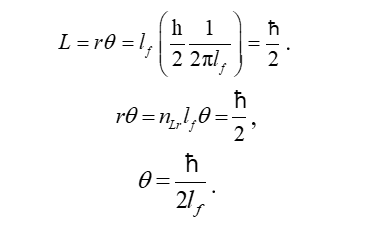—————————— read pre-print on research gate (new window) ——————————

• θ_si can be measured as the polarization angle of quantum entangled X-rays at the degenerate frequency of a maximal Bell state. As an angle θ_si=3.26239 rad ± 2 μrad; as a momentum θ_si=3.26239030392(48) kg m s^-1 and with respect to the Target Frame, θ_si has no units. The relation of angle and mass is mathematically demonstrated, as well, by No-Ping Chen, et. al.
• l_f, m_f and t_f are the fundamental measures, more precise expressions for Planck’s units – length, mass, and time – that consider the effects of length contraction associated with discrete measure.
• G is the gravitational constant, 6.6740779428(56) 10^-11m³kg^-1s^-2 such that its value considers the effects of length contraction associated with discrete measure at the upper count limit. Italicized G identifies a measure not at the limit (e.g., G=6.6738448362(53) 10^-11m³kg^-1s^-2 at the blackbody demarcation).
• c is the speed of light which may also be written as c=n_Ll_f/n_Tt_f=299,792,458 m/s such that n_L=n_T=1 is physically significant.
• ħ is the reduced Planck constant, 1.054571817 10^-34 m² kg s^-1. When accounting for the Informativity differential at the upper count bound, this term is not italicized (i.e., ħ=1.0545349844(45) ^-34 m² kg s^-1).

There are no additional terms.

The fundamental constant θ_si carries the units of angle, momentum or no units at all depending on the frame of reference and approach to the description of a phenomenon. For example, Planck’s constant and the reduced Planck constant both describe a quantum of electromagnetic action, the latter incorporating an angular property described by 2π. We propose that the fundamental constant also represents a physical anomoly, a convergence of dimensions such that all measures are the same. The relation can be demonstrated mathematically and measured.

Prerequisite to this discussion, we briefly mention that Measurement Quantization (MQ) recognizes three frames: the Reference and discrete Measurement frames of the observer, and the non-discrete Target Frame of the universe. In that the universe has no external reference, we recognize that it cannot be discrete; it is self-defining.

Frames of reference are important when working with the fundamental constant θ_si. Expressions defined with respect to the Measurement Frame, θ_si will carry units of momentum. An example would include the Planck momentum, known with respect to MQ as the fundamental expression l_fm_f=2θ_sit_f.

Defined with respect to the Target Frame (for instance, the unity expression), θ_si has no units. This follows in that the Target Frame has no external reference and as such cannot offer functions described relative to the notions of length, mass, and time.

Specific to the angle of polarization associated with X-Rays at their degenerate frequency, given certain Bell states, θ_si carries the units of angle. This correlation we carry out mathematically. The relation is specific to measure at the bound. Had the correlation occurred between bounds, it would not represent a physically significant quality of our universe. That is, two mathematical ranges of values representing different dimensional qualities will have corresponding measures. Only where bounds to a range coincide, are we offered insight into the construct of the universe.

We begin with the expression for discrete gravity, replacing θ_si with the term momentum and using Planck's expression to change units c³/G with ħ/l_f² to reduce.

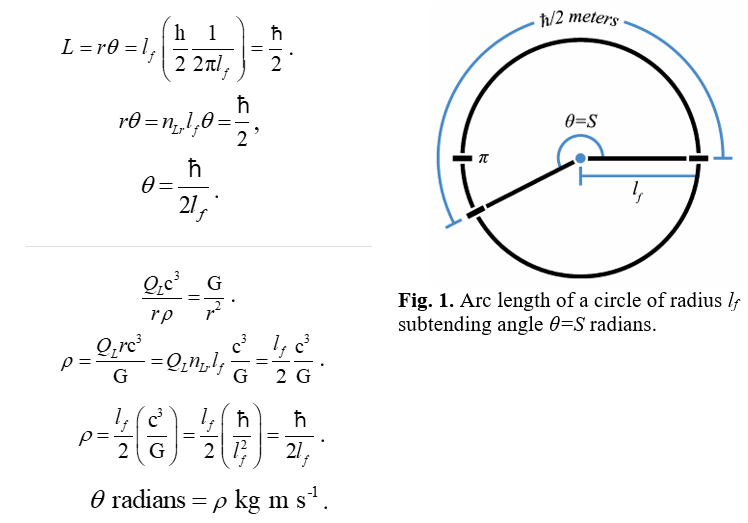
We proceed with the observation that ħ can also be defined such that we consider the arc-length of an angle equal in magnitude to Planck's constant, such that the radius is equal to the Planck length and has some angle in radians of unknown magnitude θ.

And when we combine the results of these two derivations we find that the radian measure of angle at the bound is equal to the momentum of the beam at the degenerate frequency.

As noted at the outset, we can modify this relation to easily expose Planck's unit expression for length. Why is this important? For one, application of Planck's units is a new and unfamiliar application. One might simply say we are approaching a description without physical significance. To this argument, we can counter by demonstrating the relaiton has been with us for more than one hundred years. Specifically, this is the relation described by Planck's expression for the Planck Length. Begininning with the expression for discrete gravity,

and then setting that equal to the angular description θ_si=ħ/2l_f

we resolve that:

Important, using CODATA with Planck's expressions will not provide derived values that are also consistent with other measured values. By example, solving for G using CODATA values for ħ and c will not resolve a value equal to the CODATA measure of G with the same precision. The reason as is demonstrated in the section on the fundamental measures is that Planck expressions do not incorporate the Informativity differential, a length contraction effect a property of discrete measure.

We clarify this issue by not italicizing terms when their calculated measure reflect a measure at the upper count bound. Any other measure, we italicize the term. This is noticable, for instance when working with the measures of G - which is usually measured at a macroscopic distance - and ħ, most often measured with respect to quantum phenomena such as blackbody radiation.